本章内容
定义一个基线模型
使用平均值设置基线
使用前一个时间窗口的平均值构建基线
使用前一个时间戳创建基线
实现朴素的季节性预测
在第 1 章中,我们介绍了什么是时间序列以及预测时间序列与传统回归任务的不同之处。还了解了构建成功预测项目的必要步骤,从定义目标到构建模型、部署模型以及在收集到新数据时对其进行更新。现在我们已经准备好开始预测时间序列之旅了。
您将首先学习如何对未来做出天真的预测,这将作为基准。基线模型是一个简单的解决方案,它使用启发式或简单的统计数据来计算预测。开发基线模型并不总是一门精确的科学。我们将通过可视化数据和检测那些可能用于进行预测的模式来获得一些直觉。在任何建模项目中,有一个基准很重要,因为您可以使用它来比较您将在未来构建的更复杂模型的性能。 知道模型好坏或性能好的唯一方法是将其与基线进行比较。
在本章中,假设我们希望预测强生公司的季度每股收益 (EPS)。我们可以查看图 2.1 中的数据集,它与您在第 1 章中看到的相同。具体来说,我们将使用 1960 年至 1979 年底的数据来预测 1980 年四个季度的 EPS。预测期如图 2.1 中的灰色区域所示。
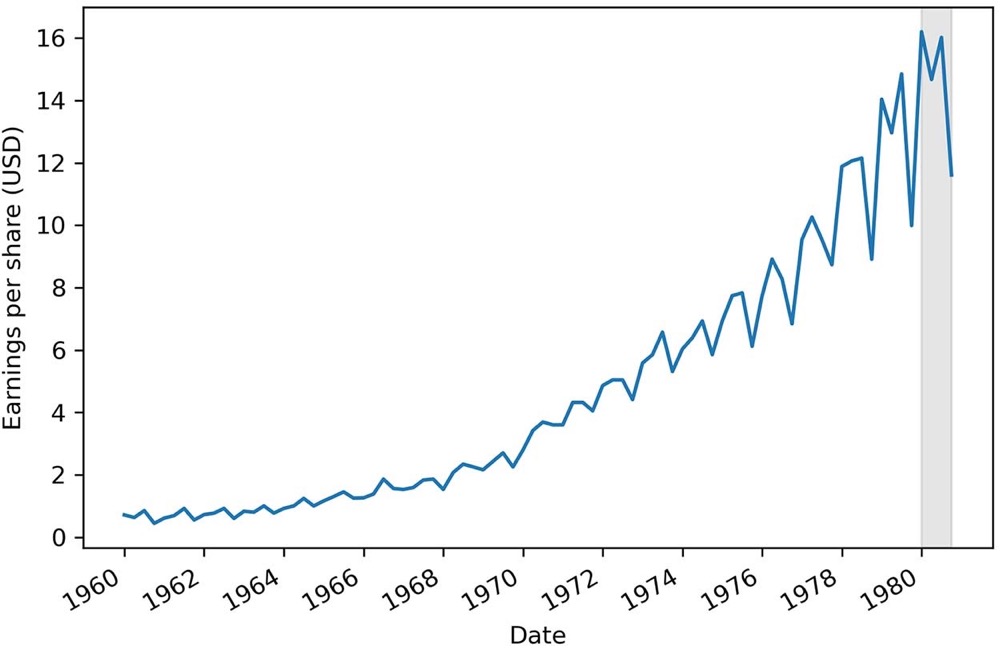
您可以在图 2.1 中看到我们的数据有一个趋势,因为它随着时间的推移而增加。此外,还存在季节性模式,因为在一年或四个季度的过程中,我们可以反复观察高峰和低谷。这意味着存在季节性。
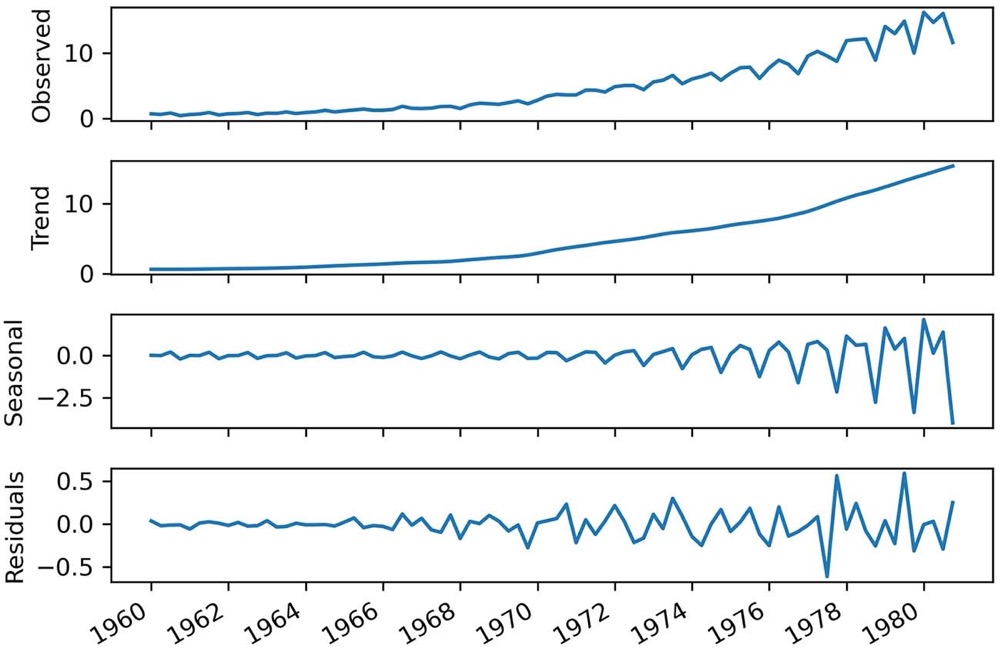
回想一下,当我们在第 1 章分解时间序列时,我们已经确定了这些组件中的每一个。组件如图 2.2 所示。 我们将在本章后面详细研究其中一些组件,因为它们将帮助我们获得对数据行为的一些直觉,进而帮助我们开发一个好的基线模型。
我们将首先定义什么是基线模型,然后我们将开发四个不同的基线来预测强生公司的季度每股收益。 现在是我们最终开始使用 Python 和进行时间序列预测的时候了。
2.1 定义基线模型
基线模型是解决我们问题的一个简单方案。它通常使用启发式或简单的统计数据来生成预测。 基线模型是您能想到的最简单的解决方案——它不需要任何培训,并且实施成本应该非常低。
你能想出我们项目的基线吗?知道我们要预测强生公司的每股收益,你能做出的最基本、最简单的预测是什么?
在时间序列的上下文中,我们可以用来构建基线的一个简单统计数据是算术平均值。 我们可以简单地计算一段时间内的值的平均值,并假设未来的值将等于该平均值。 在预测强生公司每股收益的背景下,这就像说:1960 年至 1979 年间的平均每股收益为 4.31 美元。 因此,我预计 1980 年接下来四个季度的每股收益将等于每季度 4.31 美元。
另一个可能的基线是天真地预测最后记录的数据点。 在我们的上下文中,这就像说:如果本季度的每股收益为 0.71 美元,那么下一季度的每股收益也将为 0.71 美元。
或者,如果我们在数据中看到周期性模式,我们可以简单地将这种模式重复到未来。 在当前的背景下,这就像说:如果 1979 年第一季度的每股收益为 14.04 美元,那么 1980 年第一季度的每股收益也将是 14.04 美元。
可以看到这三个可能的基线依赖于我们数据集中观察到的简单统计数据、启发式方法和模式。
基线模型
基线模型是预测问题的简单解决方案。 它依赖于启发式或简单的统计数据,通常是最简单的解决方案。 它不需要模型拟合,并且很容易实现。
您可能想知道这些基线模型是否有用。这些简单的方法能在多大程度上预测未来?我们可以通过预测 1980 年并根据 1980 年的观测数据检验我们的预测来回答这个问题。这称为样本外预测,因为我们正在对模型开发时未考虑的时期进行预测。通过这种方式,我们可以衡量模型的性能,并了解当我们预测超出现有数据(在本例中是 1981 年及以后的数据)时它们的表现如何。
在接下来的部分中,您将学习如何开发此处提到的不同基线来预测强生公司的季度每股收益。
2.2 预测历史平均值
如本章开头所述,我们将使用强生公司从 1960 年到 1980 年以美元 (USD) 表示的季度每股收益。我们的目标是使用 1960 年到 1979 年底的数据来预测 1980 年的四个季度。我们将讨论的第一个基线使用历史平均值,即过去值的算术平均值。它的实现很简单:计算训练集的平均值,这将是我们对 1980 年四个季度的预测。不过,首先,我们需要做一些我们将在所有基线实现中使用的初步工作。
2.2.1 基线实现的基本设置
我们的第一步是加载数据集。 为此,我们将使用 pandas 库并使用 read_csv 方法将数据集加载到 DataFrame 中。 您可以在本地计算机上下载文件并将文件的路径传递给 read_csv 方法,或者只需输入 CSV 文件托管在 GitHub 上的 URL。在本案例中,我们将使用该文件:
import pandas as pd
df = pd.read_csv('../data/jj.csv')注意:本章的全部代码可以在 GitHub 上找到:https://github.com/marcopeix/TimeSeriesForecastingInPython/tree/master/CH02
DataFrame 是 pandas 中最常用的数据结构。 它是一种二维标记数据结构,其列可以保存不同类型的数据,例如字符串、整数、浮点数或日期。
我们的第二步是将数据拆分为用于训练的训练集和用于测试的测试集。鉴于我们的范围是 1 年,我们的训练集将从 1960 年开始,一直到 1979 年底。为我们的测试集保存 1980 年收集的数据。您可以将 DataFrame 视为具有列名和行索引的表格或电子表格。
要查看 DataFrame 中的数据集,我们可以通过运行以下代码显示前五个条目:
df.head()将得到如图2.3所示的输出
我们可以选择显示数据集的最后五个条目并获得图 2.4 中的输出:
df.tail()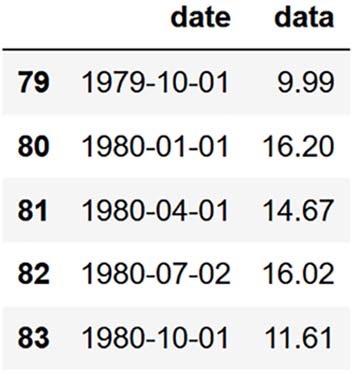
在这里,我们可以看到 1980 年的四个季度,我们将尝试使用不同的基线模型进行预测。 我们会将我们的预测与 1980 年的观测数据进行比较,以评估每个基线的表现。
在图 2.4 中,我们看到了 1980 年的四个季度,这是我们将尝试使用我们的基线模型来预测的。 我们将通过将我们的预测与 1980 年四个季度的数据列中的值进行比较来评估我们的基线表现。我们的预测越接近观察值越好。
开发基线模型之前的最后一步是将数据集拆分为训练集和测试集。 如前所述,训练集将包含 1960 年至 1979 年底的数据,而测试集将包含 1980 年的四个季度。训练集将是我们用于开发模型的唯一信息。 建立模型后,我们将预测接下来的四个时间步长,这将对应于我们测试集中 1980 年的四个季度。 这样,我们可以将我们的预测与观察到的数据进行比较,并评估我们基线的性能。
为了进行拆分,我们将指定我们的训练集将包含df中保存的所有数据,除了最后4个条目。测试集将仅由最后4个条目组成。 这是下一个代码块的作用:
train = df[:-4]
test = df[-4:]2.2.2 实现历史平均基线
现在我们准备好实现我们的基线了。首先使用整个训练集的算术平均值。 为了计算平均值,我们将使用 numpy 库,因为它是一个非常快速的 Python 科学计算包,与 DataFrame 配合得非常好:
import numpy as np
historical_mean = np.mean(train['data']) # 计算训练集中数据列的算术平均值。
print(historical_mean)在前面的代码块中,我们首先导入 numpy 库,然后计算整个训练集的 EPS 平均值并将其打印在屏幕上。输出结果为 4.31 美元。 这意味着从 1960 年到 1979 年底,强生公司的季度每股收益平均为 4.31 美元。
现在我们将天真地预测 1980 年每个季度的这个值。为此,我们将简单地创建一个新列 pred_mean,它将训练集的历史平均值作为预测:
test.loc[:, 'pred_mean'] = historical_mean # 把历史数据的平均值设置为预测值接下来,我们需要定义和计算一个误差指标,以评估我们在测试集上的预测性能。 在这里我们将使用平均绝对百分比误差 (MAPE,Mean Absolute Percentage Error)。这意味着无论我们使用两位数还是六位数,MAPE 将始终以百分比表示。因此,MAPE 返回预测值平均偏离观测值或实际值的百分比,无论预测值高于还是低于观测值。 MAPE 在方程 2.1 中定义。
公式2.1
MAPE = \frac{1}{n} \sum_{i=1}^n | \frac{A_{i}-F_{i}}{A_{i}} | *100MAPE=n1i=1∑n∣AiAi−Fi∣∗100
公式2.1中,*Ai*为时间点i的实际值,*Fi*为时间点的预测值; n是预测的数量。本例中我们预测的是 1980 年的4个季度,所以 n = 4。在求和中,从实际值中减去预测值,然后将结果除以实际值,得到百分比误差;然后取百分比误差的绝对值。对 n 个时间点中的每一个重复此操作,并将结果相加。 最后,我们将总和除以时间点数 n,最终计算出了平均绝对百分比误差。
下面,我们在 Python 中实现这个函数。定义一个 mape 函数,它接受两个向量:y_true 表示在测试集中观察到的实际值,y_pred 表示预测值。本例中,我们使用Numpy数组,不需要循环对所有值求和。可以简单地从 y_true 数组中减去 y_pred 数组并除以 y_true 以获得百分比误差。 然后取其绝对值,==再取其结果的平均值,这将负责对向量中的每个值求和并除以预测的数量。(After that, we take the mean of the result, which will take care of summing up each value in the vector and dividing by the number of predictions. )==最后,我们将结果乘以 100,让输出以百分比而不是十进制数表示:
def mape(y_true, y_pred):
return np.mean(np.abs((y_true-y_pred) / y_true))*100现在我们可以计算基线的 MAPE。 我们的实际值在 test 的data列中,因此它将是传递给 mape 函数的第1个参数。 我们的预测在 test 的 pred_mean 列中,所以它将是函数的第2个参数:
mape_hist_mean = mape(test['data'],test['pred_mean'])
print(mape_hist_mean)运行该函数给出 70.00% 的 MAPE。 这意味着我们的基线与 1980 年观察到的强生公司季度每股收益平均偏离 70%。
接下来,让我们可视化我们的预测结果,以更好地了解我们 70% 的 MAPE。
Listing 2.1 Visualizing our forecasts
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(train['date'],train['data'], 'g-.', label='Train')
ax.plot(test['date'],test['data'], 'b-.', label='Test')
ax.plot(test['date'],test['pred_mean'], 'r--', label='Predicted')
ax.set_xlabel('Date')
ax.set_ylabel('Earnings per share (USD)')
ax.axvspan(80,83,color='#808080',alpha=0.2)
ax.legend(loc=2)
plt.xticks(np.arange(0, 85, 8), [1960, 1962, 1964, 1966, 1968, 1970, 1972, 1974, 1976, 1978, 1980])
fig.autofmt_xdate()
plt.tight_layout()在清单 2.1 中,我们使用 matplotlib 库(它是 Python 中最流行的用于生成可视化的库)生成一个图表,显示训练数据、预测范围、测试集的观察值以及 1980 年每个季度的预测。
首先,我们初始化一个figure和一个 ax 对象。 一个图形可以包含许多 ax 对象,这允许我们创建一个包含两个、三个或更多绘图的图形。 在这种情况下,我们正在创建一个带有单个图的图形,因此我们只需要一个 ax。
其次,我们将数据绘制在 ax 对象上。我们使用绿色虚线和点划线绘制train数据,并给这条曲线一个标签“Train”。该标签稍后可用于生成图表的图例。然后我们绘制test数据并使用带有“Test”标签的蓝色连续曲线。最后,我们使用带有“Predicted”标签的红色虚线绘制了我们的预测值曲线。
第三,通过标记x 轴和 y 轴绘制一个矩形区域来说明预测范围。因为我们的预测范围是 1980 年的四个季度,所以该区域应该从索引 80 开始,到索引 83 结束,跨越 1980 年全年。请记住,我们通过运行 df.tail() 获得了 1980 年最后一个季度的指数,结果如图 2.5所示。
我们将这个区域设备为灰色,并使用 alpha 参数指定不透明度。 当 alpha 为 1 时,形状完全不透明; 当 alpha 为 0 时,它是完全透明的。 在我们的例子中,将使用 20% 或 0.2 的不透明度。
然后我们为 x 轴上的刻度指定标签。默认情况下,标签将显示数据集每个季度的数据,这将创建一个非常拥挤且难易辨识的 x 轴标签。相反,我们将每 2 年显示一次年份。为此,我们将生成一个数组,指定标签必须出现的索引。这就是 np.arange(0, 81, 8) 的作用:它生成一个从 0 开始,到 80 结束的数组,因为不包括结束索引 (81),步长为 8,因为 2 年内有 8 个季度。这将有效地生成以下数组:[0,8,16,...72,80]。然后指定一个包含每个索引处标签的数组,因此它必须以 1960 开始并以 1980 结束,就像我们的数据集一样。
最后,我们使用 fig.automft_xdate() 来自动格式化 x 轴上的刻度标签。 它会稍微旋转它们并确保它们清晰易读。 最后使用 plt.tight_layout() 删除图形周围的任何多余空白。
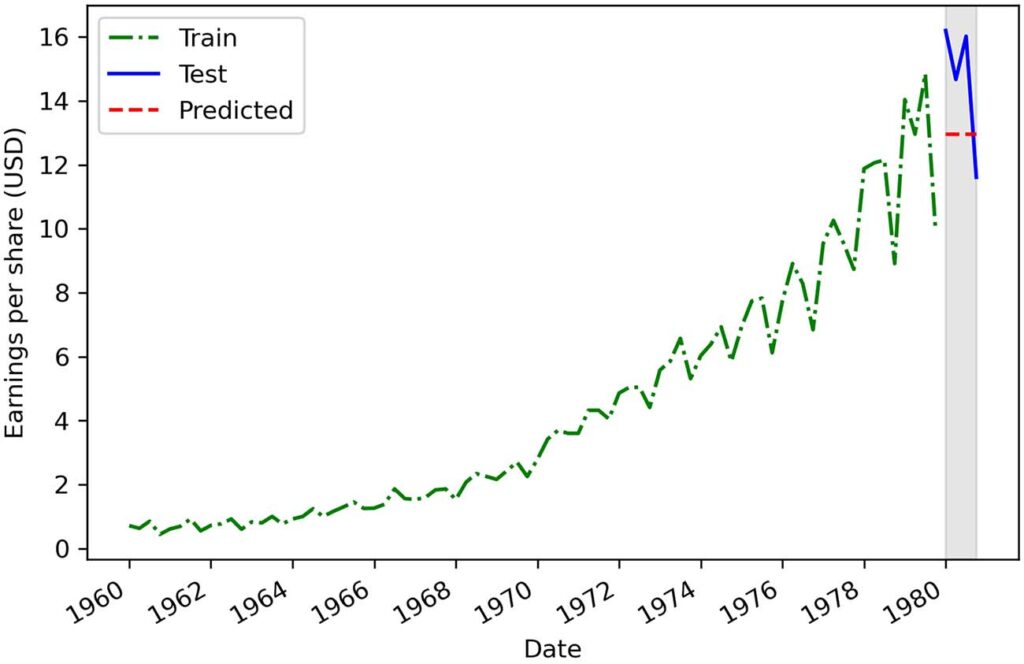
最终结果如图 2.6。 显然,这个基线没有产生准确的预测,因为预测线离测试线很远。现在我们知道,我们的预测平均比 1980 年每个季度的实际每股收益低 70%。尽管 1980 年的每股收益一直高于 10 美元,但我们预测每个季度仅为 4.31 美元。
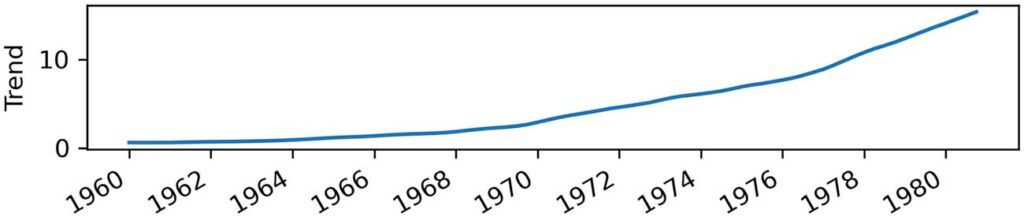
不过,我们能从中学到什么? 查看我们的训练集,我们可以看到一个积极的趋势,因为 EPS 随着时间的推移而增加。 来自我们数据集分解的趋势分量进一步支持了这一点,如图 2.7 所示。
正如你所看到的,我们不仅有趋势,而且趋势在 1960 年到 1980 年之间并不是恒定的——它变得越来越陡峭。 因此,1960 年观察到的 EPS 可能无法预测 1980 年的 EPS,因为我们有一个积极的趋势,EPS 值随着时间的推移而增加,并且以更快的速度增加。
你能改善我们的基线吗?
在继续下一部分之前,你能想出一种方法来改进我们的基线,同时仍然使用平均值吗? 你认为取更短和更近的时间段的平均值会有所帮助吗(例如,从 1970 年到 1979 年)?
2.3 预测去年的平均值
从之前的基线中吸取的教训是,由于我们数据集中的积极趋势成分,早期的值似乎不能预测未来长期的值。早期的值似乎太小,无法代表 EPS 在 1979 年底和 1980 年达到的新水平。
如果我们在训练集中使用去年的平均值来预测下一年呢? 这意味着我们将计算 1979 年的平均每股收益,并预测 1980 年每个季度的每股收益——随着时间的推移而增加的最近的值可能更接近 1980 年观察到的值。目前,这只是一个假设, 所以让我们实现这个基线并测试它,看看它是如何执行的。
我们的数据已经分为测试集和训练集(在第 2.2.1 节中完成),因此我们可以继续计算训练集中最后一年的平均值,对应于 1979 年的最后四个数据点:
last_year_mean = np.mean(train[-4:]) # 计算1979年四个季度的平均 EPS,它们是训练集的最后四个数据点。
print(last_year_mean)通过计算得出平均每股收益为 12.96 美元。 因此,我们将预测强生公司在 1980 年四个季度的每股收益为 12.96 美元。使用我们用于上一个基线的相同程序,我们将创建一个新的 pred_last_yr_mean 列来保存去年的平均值 我们的预测:
test.loc[:, 'pred_last_yr_mean'] = last_year_mean然后,使用我们之前定义的 mape 函数,可以评估新基线的性能。请记住,第一个参数是观察值,保存在测试集中。 然后我们传入预测值,它们pred_last_yr_mean 列:
mape_last_year_mean = mape(test['data'], test['pred__last_yr_mean'])
print(mape_last_year_mean)我们得到了 15.60% 的 MAPE。 我们可以在图 2.8 中可视化我们的预测。
你能重现图 2.8 吗?
作为练习,尝试重新创建图 2.8,以使用 1979 年各季度的平均值来可视化预测。代码应该与清单 2.1 相同,只是这次预测位于不同的列中。

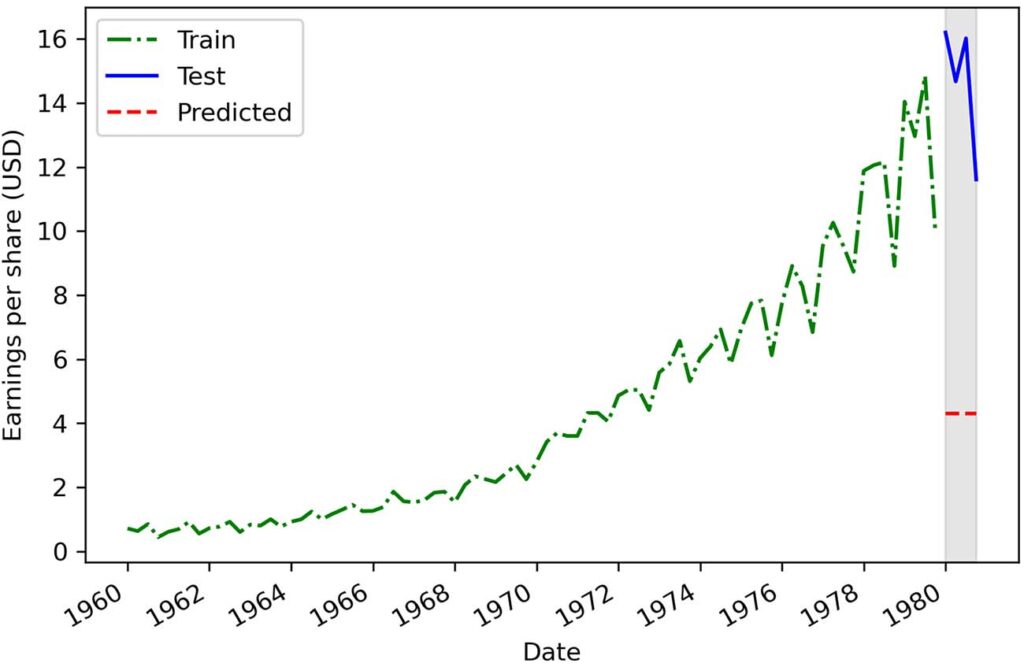
这个新基线比之前的基线有了明显的改进,尽管它的实现同样简单,因为我们将 MAPE 从 70% 降低到 15.6%。这意味着我们的预测平均偏离观测值 15.6%。 使用去年的平均值是朝着正确方向迈出的一大步。我们希望 MAPE 尽可能接近 0%,因为这将转化为更接近我们预测范围内实际值的预测。
我们可以从这个基线中了解到,未来的价值可能取决于历史上不太远的过去价值。这里涉及到了自相关的内容,我们将在第 5 章深入探讨这个主题。现在,让我们看看我们可以针对这种情况开发的另一个基线。
2.4 使用最后一个已知值进行预测
之前,我们使用不同时期的平均值来开发基线模型。 到目前为止,最好的基线是我们训练集中最后记录年份的平均值,因为它产生了最低的 MAPE。 我们从该基线中了解到,未来的价值取决于过去的价值,而不是那些太远的时间。事实上,预测 1960 年至 1979 年的平均每股收益比预测 1979 年的平均每股收益更差。
因此,我们可以假设使用训练集的最后一个已知值作为基线模型会给我们更好的预测,这将转化为接近 0% 的 MAPE。 让我们检验这个假设。
第一步是提取我们训练集的最后一个已知值,它对应于 1979 年最后一个季度记录的 EPS:
last = train.data.iloc[-1]
print(last) # 9.99当我们检索 1979 年最后一个季度记录的 EPS 时,我们得到 9.99 美元的值。 因此,我们将预测强生公司 1980 年四个季度的每股收益为 9.99 美元。
同样,我们将追加一个名为 pred_last 的新列来保存预测。
test.loc[:, 'pred_last'] = last然后,使用我们之前定义的相同 MAPE 函数,我们可以评估这个新基线模型的性能。 同样,我们将来自测试集的实际值和来自测试 pred_last 列的预测传递给函数:
mape_last = mape(test['data'], test['pred_last'])
print(mape_last)这给了我们 30.45% 的 MAPE。 我们可以将图 2.9 中的预测可视化。
你能重现图 2.9 吗?
尝试自己制作图 2.9! 作为数据科学家,对我们来说,以不在我们领域工作的人可以访问的方式传达我们的结果非常重要。 因此,制作显示我们预测的图表是一项重要的技能开发。
似乎我们的新假设在我们建立的最后一个基线上没有改进,因为我们的 MAPE 为 30.45%,而我们使用 1979 年的平均 EPS 实现了 15.60% 的 MAPE。因此,这些新的预测与 1980 年的观测值相去甚远。
这可以通过 EPS 表现出周期性行为来解释,在前三个季度它很高,然后在最后一个季度下降。 使用最后一个已知值没有考虑季节性,因此我们需要使用另一种简单的预测技术来看看我们是否可以产生更好的基线。
2.5 实现一个朴素的季节性预测
我们在本章中考虑了前两个基线的趋势分量,但我们没有研究数据集中的另一个重要分量,即图 2.10 所示的季节性分量。 我们的数据中有明显的周期性模式,这是我们可以用来构建最后一个基线的一条信息:朴素的季节性预测。
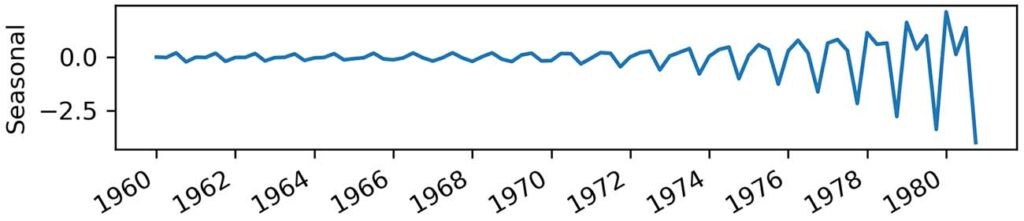
朴素的季节性预测采用最后观察到的周期并将其重复到未来。在我们的例子中,一个完整的周期发生在四个季度,因此我们将采用 1979 年第一季度的 EPS 并预测 1980 年第一季度的值。然后我们将采用 1979 年第二季度的 EPS 并预测 1980 年第二季度的值。这个过程将在第三和第四季度重复。
在 Python 中,我们可以通过简单地获取训练集的最后四个值来实现这个基线,它们对应于 1979 年的四个季度,并将它们分配给 1980 年的相应季度。下面的代码附加了 pred_last_season 列来保存 我们从朴素的季节性预测方法中做出的预测:
test.loc[:, 'pred_last_season'] = train['data'][-4:].values # 我们的预测值是我们训练集的最后四个值,对应于 1979 年的季度。然后我们以与前面部分相同的方式计算 MAPE:
mape_naive_seasonal = mape(test['data'], test['pred_last_season'])
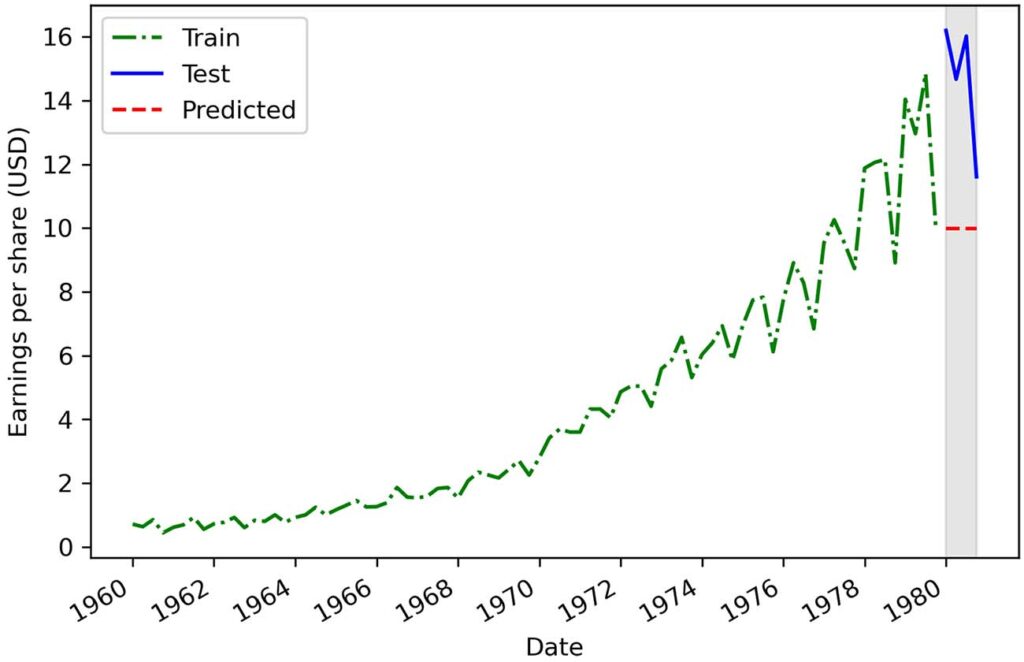
print(mape_naive_seasonal) # 11.56这给了我们 11.56% 的 MAPE,这是本章所有基线中最低的 MAPE。 图 2.11 说明了我们的预测与测试集中观察到的数据的比较。 作为练习,我强烈建议您尝试自己重新创建它。
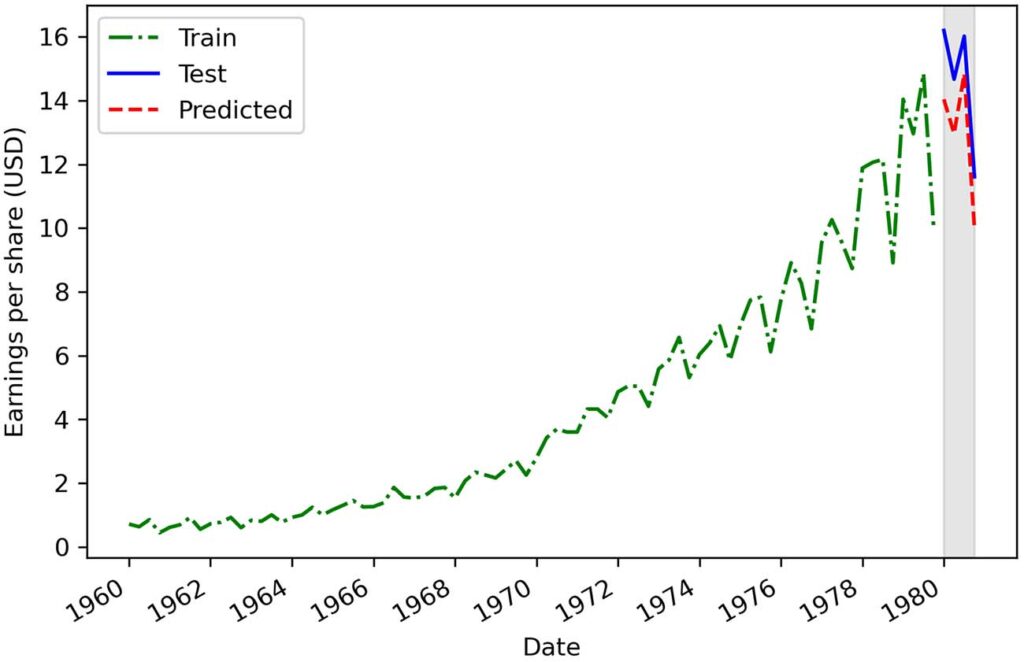
这个预测更类似于在测试集中观察到的数据,它导致了最低的 MAPE。 显然,该数据集的季节性对未来值有影响,在预测时必须加以考虑。
如您所见,我们幼稚的季节性预测导致我们在本章中建立的所有基线中的最低 MAPE。 这意味着季节性对未来值有重大影响,因为将上一个季节重复到未来会产生相当准确的预测。 直观地说,这是有道理的,因为我们可以清楚地观察到图 2.11 中每年都在重复的周期性模式。 当我们为这个问题开发更复杂的预测模型时,必须考虑季节性影响。 我将在第 8 章详细解释如何解释它们。
2.6 下一步
在本章中,我们为我们的预测项目开发了四个不同的基线。 我们使用了整个训练集的算术平均值、训练集中最后一年的平均值、训练集的最后一个已知值以及一个幼稚的季节预测。 然后使用 MAPE 指标在测试集上评估每个基线。 图 2.12 总结了我们在本章中开发的每个基线的 MAPE。 如您所见,使用朴素季节性预测的基线具有最低 MAPE,因此性能最佳。
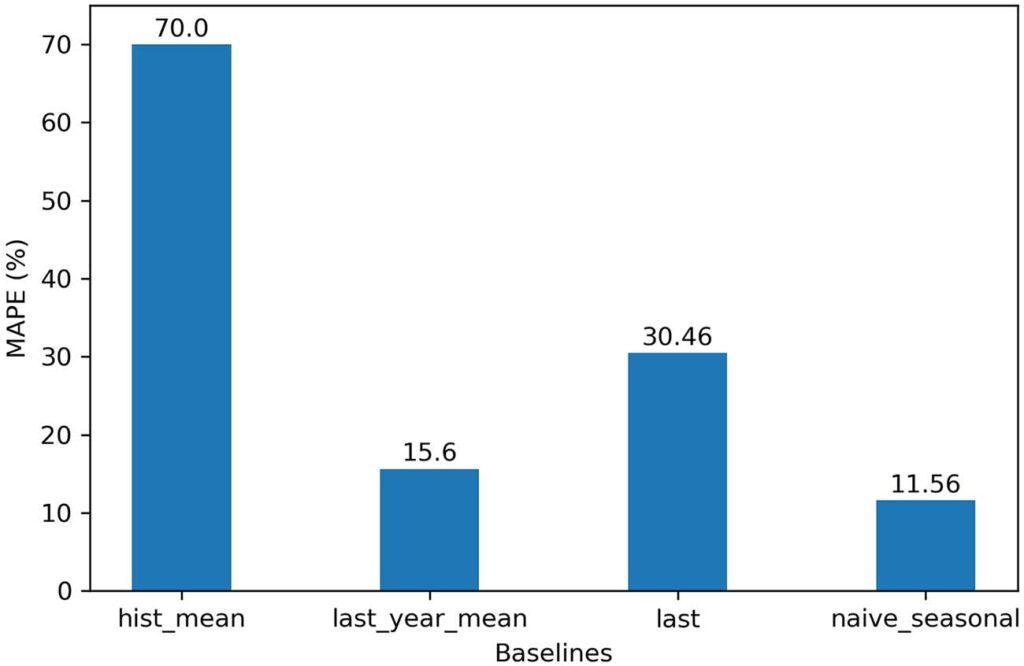
请记住,基线模型可作为比较的基础。我们将通过应用统计学习或深度学习技术开发更复杂的模型,当我们根据测试集评估更复杂的解决方案并记录我们的错误指标时,我们可以将它们与基线进行比较。在我们的例子中,我们会将复杂模型的 MAPE 与我们幼稚的季节性预测的 MAPE 进行比较。如果一个复杂模型的 MAPE 低于 11.56%,那么我们就会知道我们有一个性能更好的模型。
在某些特殊情况下,只能使用幼稚的方法来预测时间序列。这些是过程随机且无法使用统计学习方法预测的特殊情况。这意味着存在随机性——我们将在下一章探讨这一点。
本章概要
时间序列预测从基线模型开始,该模型用作与更复杂模型进行比较的基准。
基线模型是我们预测问题的一个简单的解决方案,因为它只使用启发式或简单的统计数据,例如平均值。
MAPE 代表平均绝对百分比误差,它是预测值与实际值的偏差程度的直观度量。
有很多方法可以制定基线。 在本章中,您了解了如何使用均值、最后一个已知值或上一个季节。
发表回复